10 4/13 Lab IX | Time Series

## Packages
library(haven)
library(AER)
library(orcutt)
library(tidyverse)
library(lubridate)
library(lmtest)
library(sandwich)

## Loading Data
load("~/GOVT702/Data/Ch13_Lab_GasPrices.RData")

Data description:

Variable	Description
year	Year
month	Month
time	Time identifier (1 for first observation, etc)
logMilesNA	Log of vehicle miles traveled (in millions) in the U.S., not seasonally adjusted
logLightTruckSales	Log of retail sales of light weight trucks in the U.S. (in thousands)
logGasReal	Log of real price of gas
unem	Unemployment rate
logPop	Log of U.S. population (in thousands)

10.1 Estimate a model with the log of miles driven (use the unadjusted data: logMilesNA) as a function of log gas prices, unemployment and log of population. (Don’t account for autocorrelation.) Is the effect of gas statistically significant?

## Model 1
reg.1 <- dta %>%
  lm(logMilesNA ~ logGasReal + unem + logPop, data = .)

## Summary Output
summary(reg.1)

## 
## Call:
## lm(formula = logMilesNA ~ logGasReal + unem + logPop, data = .)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.195230 -0.045729  0.004914  0.051965  0.136480 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -5.918752   1.065393  -5.555 6.11e-08 ***
## logGasReal   0.030388   0.021152   1.437    0.152    
## unem        -0.019785   0.002654  -7.455 9.67e-13 ***
## logPop       1.461736   0.084586  17.281  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.06833 on 300 degrees of freedom
##   (260 observations deleted due to missingness)
## Multiple R-squared:  0.7243, Adjusted R-squared:  0.7215 
## F-statistic: 262.7 on 3 and 300 DF,  p-value: < 2.2e-16

## 95% CI
confint(reg.1)

##                   2.5 %      97.5 %
## (Intercept) -8.01534205 -3.82216115
## logGasReal  -0.01123688  0.07201218
## unem        -0.02500777 -0.01456290
## logPop       1.29527941  1.62819344

10.2 Do you think there is seasonality in driving? Test by adding dummy variables for month to the above model. Is there evidence of monthly variation? Is the effect of gas statistically significant? Now create a categorical variable for seasons and run the model without the month dummy variable.

## Removing NAs
dta <- dta %>%
  drop_na()

## Creating a variable for seasons
dta <- dta %>%
  mutate(season = case_when(
    month == 1 | month == 2 | month == 3 ~ "Winter",
    month == 4 | month == 5 | month == 6 ~ "Spring",
    month == 7 | month == 8 | month == 9 ~ "Summer",
    month == 10 | month == 11 | month == 12 ~ "Fall")
    )

## Model 2 Months
reg.2a <- dta %>%
  lm(logMilesNA ~ logGasReal + unem + logPop + factor(month), data = .)

## Summary Output
summary(reg.2a)

## 
## Call:
## lm(formula = logMilesNA ~ logGasReal + unem + logPop + factor(month), 
##     data = .)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.078372 -0.017092  0.000947  0.019921  0.058033 
## 
## Coefficients:
##                  Estimate Std. Error t value Pr(>|t|)    
## (Intercept)     -8.432427   0.443617 -19.008  < 2e-16 ***
## logGasReal      -0.042114   0.008961  -4.700 4.04e-06 ***
## unem            -0.014137   0.001122 -12.603  < 2e-16 ***
## logPop           1.651863   0.035166  46.974  < 2e-16 ***
## factor(month)2  -0.047461   0.007907  -6.003 5.81e-09 ***
## factor(month)3   0.099815   0.007933  12.583  < 2e-16 ***
## factor(month)4   0.093377   0.008030  11.628  < 2e-16 ***
## factor(month)5   0.142644   0.008063  17.690  < 2e-16 ***
## factor(month)6   0.144017   0.008003  17.995  < 2e-16 ***
## factor(month)7   0.169429   0.007981  21.228  < 2e-16 ***
## factor(month)8   0.165200   0.008007  20.633  < 2e-16 ***
## factor(month)9   0.074265   0.007976   9.311  < 2e-16 ***
## factor(month)10  0.113230   0.007960  14.224  < 2e-16 ***
## factor(month)11  0.042180   0.007915   5.329 1.99e-07 ***
## factor(month)12  0.050981   0.007893   6.459 4.45e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.02795 on 289 degrees of freedom
## Multiple R-squared:  0.9556, Adjusted R-squared:  0.9534 
## F-statistic:   444 on 14 and 289 DF,  p-value: < 2.2e-16

## 95% CI
confint(reg.2a)

##                       2.5 %      97.5 %
## (Intercept)     -9.30555634 -7.55929713
## logGasReal      -0.05975083 -0.02447708
## unem            -0.01634434 -0.01192881
## logPop           1.58264989  1.72107617
## factor(month)2  -0.06302371 -0.03189915
## factor(month)3   0.08420205  0.11542848
## factor(month)4   0.07757182  0.10918316
## factor(month)5   0.12677323  0.15851447
## factor(month)6   0.12826530  0.15976855
## factor(month)7   0.15372049  0.18513846
## factor(month)8   0.14944155  0.18095910
## factor(month)9   0.05856676  0.08996317
## factor(month)10  0.09756222  0.12889798
## factor(month)11  0.02660157  0.05775803
## factor(month)12  0.03544623  0.06651523

## Model 2 Seasons
reg.2b <- dta %>%
  lm(logMilesNA ~ logGasReal + unem + logPop + factor(season), data = .)

## Summary Output
summary(reg.2b)

## 
## Call:
## lm(formula = logMilesNA ~ logGasReal + unem + logPop + factor(season), 
##     data = .)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.139222 -0.040786  0.004486  0.035948  0.140897 
## 
## Coefficients:
##                       Estimate Std. Error t value Pr(>|t|)    
## (Intercept)          -7.832131   0.806242  -9.714  < 2e-16 ***
## logGasReal           -0.026933   0.016238  -1.659   0.0983 .  
## unem                 -0.014513   0.002033  -7.137 7.33e-12 ***
## logPop                1.609829   0.063964  25.168  < 2e-16 ***
## factor(season)Spring  0.056839   0.008335   6.819 5.12e-11 ***
## factor(season)Summer  0.065784   0.008295   7.931 4.46e-14 ***
## factor(season)Winter -0.050893   0.008424  -6.042 4.56e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.05104 on 297 degrees of freedom
## Multiple R-squared:  0.8477, Adjusted R-squared:  0.8446 
## F-statistic: 275.5 on 6 and 297 DF,  p-value: < 2.2e-16

## 95% CI
confint(reg.2b)

##                            2.5 %       97.5 %
## (Intercept)          -9.41880203 -6.245459970
## logGasReal           -0.05888954  0.005024539
## unem                 -0.01851452 -0.010511204
## logPop                1.48394893  1.735709462
## factor(season)Spring  0.04043612  0.073242797
## factor(season)Summer  0.04946019  0.082107980
## factor(season)Winter -0.06747086 -0.034315628

10.3 Briefly explain why there might be autocorrelation.

With 50 years of data, there are certainly time trends and we can reasonably expect the error term of one year to be correlated with the error term of the previous year. For example, if more people began longer commutes in the 1990s, the longer commutes (more miles driven) will continue into the 2000s so the errors will be correlated year by year.

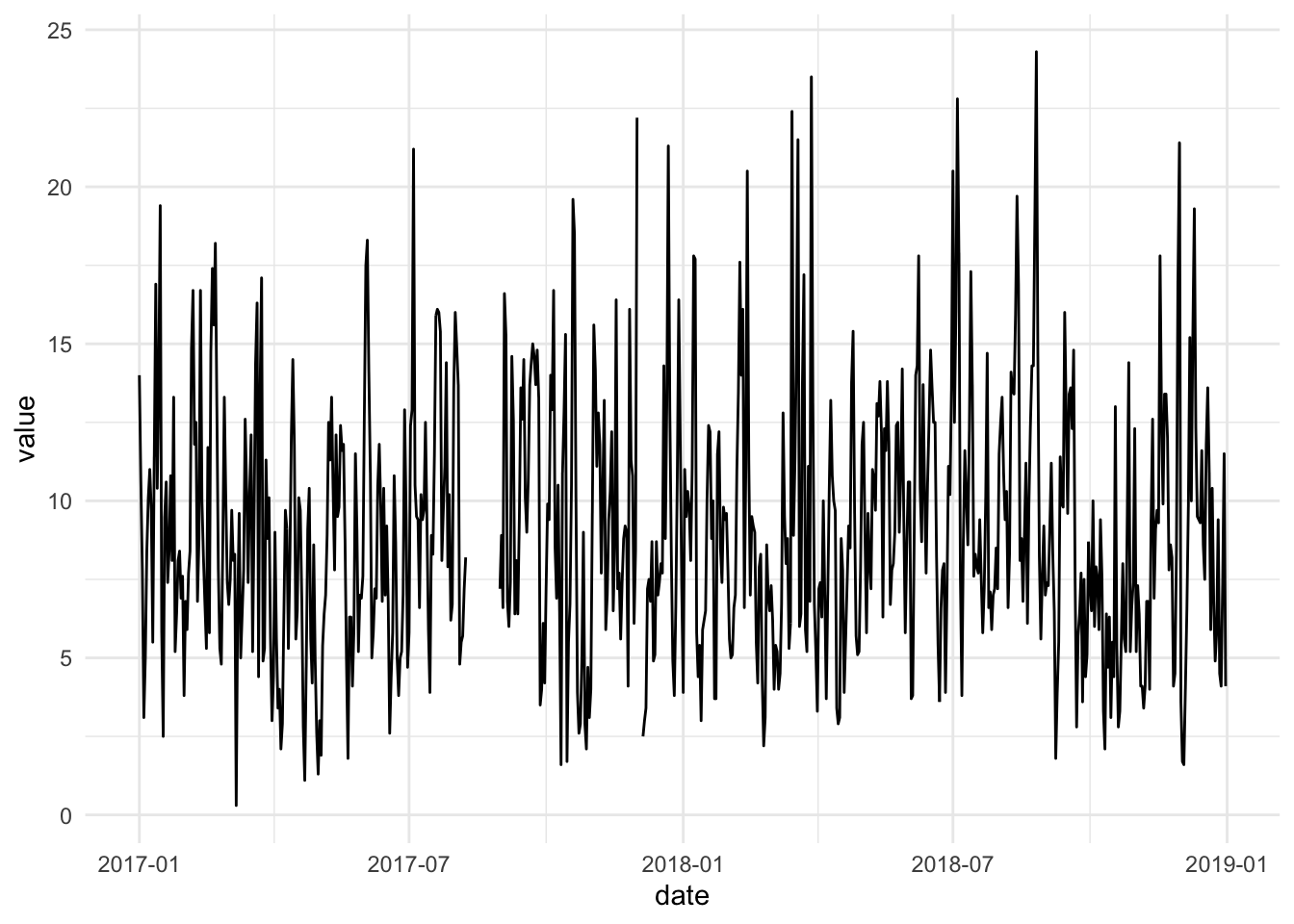
10.4 Create a figure that is useful to assess whether there is autocorrelation (you have two choices here). Draw a sketch here.

## Saving the Residuals
dta$residual_errors  <- resid(reg.2a)

## Regressing Residuals
lag_err <- c(NA, dta$residual_errors[1:(length(dta$residual_errors)-1)])

plot(lag_err, dta$residual_errors, pch=20, xlab = "Lagged Residuals", 
     ylab = "Residuals", bty="n", col="dark blue", las=1)
abline(lm(dta$residual_errors ~ lag_err), lwd=2)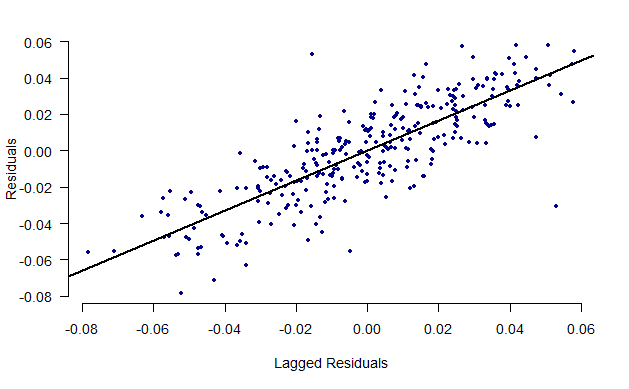

## Plotting Over Time
plot(dta$residual_errors, pch=20, xlab = "Time", las=1, 
     ylab = "Residuals", bty="n", col="dark blue")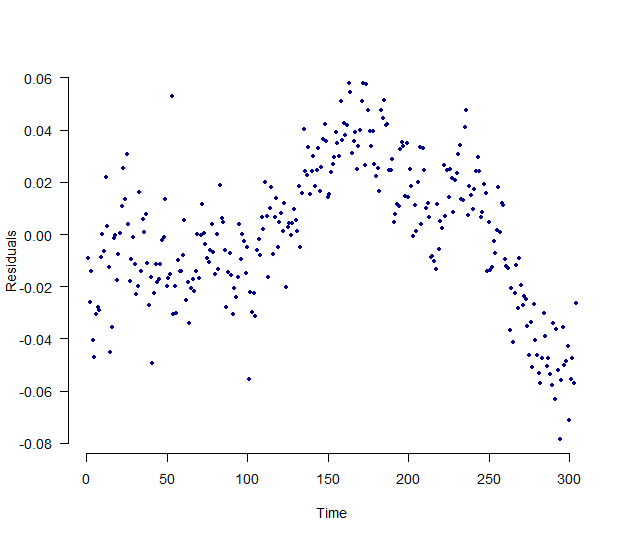

# Creating season category and plotting residual error
dta %>% 
  ggplot() +
  geom_line(aes(x=as.Date(date), y=residual_errors, col=season), size=.8) +
  scale_color_manual(values=c("orange", "green", "red", "darkblue"))+
  labs(x="Date", y="Residual Errors") +
  theme_classic() +
  theme(panel.grid.major.y=element_line(color="darkgrey", linetype="dotted"), panel.grid.minor.y=element_line(color="darkgrey", linetype="dotted")) %>%
  labs(col="Season")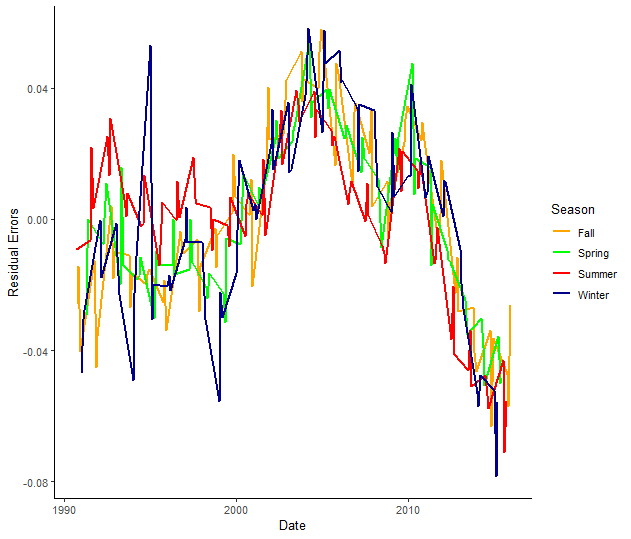

# Creating season category and plotting residual error
dta %>% 
  ggplot() +
  geom_point(aes(x=as.Date(date), y=residual_errors, col=season)) +
  scale_color_manual(values=c("orange", "green", "red", "darkblue"))+
  labs(x="Date", y="Residual Errors") +
  theme_classic() +
  theme(panel.grid.major.y=element_line(color="darkgrey", linetype="dotted"), panel.grid.minor.y=element_line(color="darkgrey", linetype="dotted")) %>%
  labs(col="Season")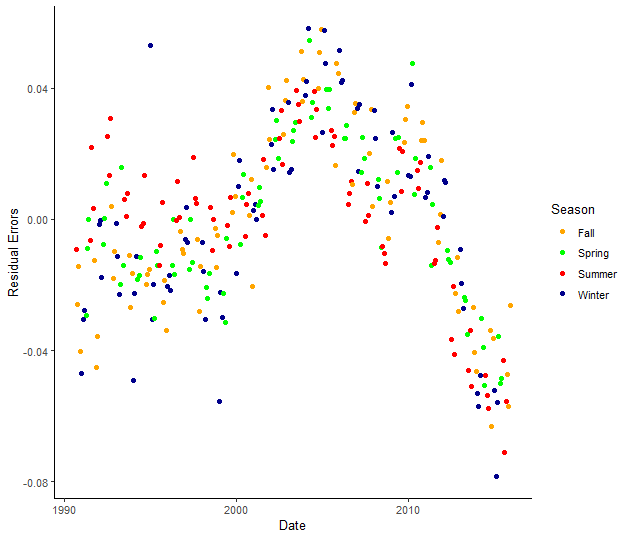

10.5 Test whether there is first order autocorrelation. Report the key statistic from this test. What would a coefficient of 1 indicate?

## Error on Lagged Error Regression
reg.lag <- lm(dta$residual_errors ~ lag_err)
summary(reg.lag)

## 
## Call:
## lm(formula = dta$residual_errors ~ lag_err)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.074188 -0.010223  0.001141  0.010386  0.065748 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -4.056e-05  8.993e-04  -0.045    0.964    
## lag_err      8.215e-01  3.300e-02  24.892   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.01565 on 301 degrees of freedom
##   (1 observation deleted due to missingness)
## Multiple R-squared:  0.673,  Adjusted R-squared:  0.6719 
## F-statistic: 619.6 on 1 and 301 DF,  p-value: < 2.2e-16

## Durbin-Watson
dwtest(reg.2a)

## 
##  Durbin-Watson test
## 
## data:  reg.2a
## DW = 0.35861, p-value < 2.2e-16
## alternative hypothesis: true autocorrelation is greater than 0

10.6 Use Newey-West standard errors to account for autocorrelation. Use the same variables as in part (b). Determine the t-stats and describe the similarities and difference with earlier results.

## Calculating Newey West Standard Errors
sqrt(diag(NeweyWest(reg.2a, lag=4, prewhite=FALSE, adjust=TRUE)))

##     (Intercept)      logGasReal            unem          logPop  factor(month)2  factor(month)3  factor(month)4  factor(month)5 
##     1.038631354     0.017795927     0.001853709     0.082605874     0.005951753     0.006987587     0.008119800     0.008298968 
##  factor(month)6  factor(month)7  factor(month)8  factor(month)9 factor(month)10 factor(month)11 factor(month)12 
##     0.008732203     0.008721058     0.008926142     0.008676850     0.007994856     0.007639009     0.006481667

## Checking t-stats
coef(reg.2a) / sqrt(diag(NeweyWest(reg.2a, lag=4, prewhite=FALSE, adjust=TRUE)))

##     (Intercept)      logGasReal            unem          logPop  factor(month)2  factor(month)3  factor(month)4  factor(month)5 
##       -8.118787       -2.366494       -7.626101       19.996920       -7.974362       14.284654       11.499973       17.188144 
##  factor(month)6  factor(month)7  factor(month)8  factor(month)9 factor(month)10 factor(month)11 factor(month)12 
##       16.492622       19.427629       18.507471        8.558977       14.162868        5.521632        7.865373

10.7 Estimate a model that adjusts for autocorrelation. Use the same variables as in part (b). Describe similarities and difference with earlier results.

## Cochrane-Orcutt Model
reg.orc <- cochrane.orcutt(reg.2a)
summary(reg.orc)

## Call:
## lm(formula = logMilesNA ~ logGasReal + unem + logPop + factor(month), 
##     data = .)
## 
##                   Estimate Std. Error t value  Pr(>|t|)    
## (Intercept)     -8.5660946  1.1602976  -7.383 1.675e-12 ***
## logGasReal      -0.0545711  0.0165253  -3.302 0.0010800 ** 
## unem            -0.0106665  0.0030232  -3.528 0.0004867 ***
## logPop           1.6604913  0.0922935  17.991 < 2.2e-16 ***
## factor(month)2  -0.0467377  0.0033259 -14.053 < 2.2e-16 ***
## factor(month)3   0.1018515  0.0046115  22.087 < 2.2e-16 ***
## factor(month)4   0.0977499  0.0059402  16.456 < 2.2e-16 ***
## factor(month)5   0.1473488  0.0064157  22.967 < 2.2e-16 ***
## factor(month)6   0.1473300  0.0062046  23.745 < 2.2e-16 ***
## factor(month)7   0.1725746  0.0061698  27.971 < 2.2e-16 ***
## factor(month)8   0.1692116  0.0062837  26.929 < 2.2e-16 ***
## factor(month)9   0.0794105  0.0063119  12.581 < 2.2e-16 ***
## factor(month)10  0.1184317  0.0060001  19.738 < 2.2e-16 ***
## factor(month)11  0.0466867  0.0052127   8.956 < 2.2e-16 ***
## factor(month)12  0.0549369  0.0042181  13.024 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.0157 on 298 degrees of freedom
## Multiple R-squared:  0.9368 ,  Adjusted R-squared:  0.936
## F-statistic: 305.1 on 4 and 298 DF,  p-value: < 1.79e-163
## 
## Durbin-Watson statistic 
## (original):    0.35861 , p-value: 5.127e-46
## (transformed): 2.58848 , p-value: 1e+00

## "By Hand"
reg.2a <- dta %>%
  lm(logMilesNA ~ logGasReal + unem + logPop + factor(month), data = .)

## Error on Lagged Error Regression
reg.lag <- lm(dta$residual_errors ~ lag_err)
rho <- summary(reg.lag)$coef[2]

## Lagging Each Variable
dta$lagmile <- dplyr::lag(dta$logMilesNA, ordered_by = dta$year)
dta$lag_gas <- dplyr::lag(dta$logGasReal, ordered_by = dta$year)
dta$lag_unem <- dplyr::lag(dta$unem, ordered_by = dta$year)
dta$lag_pop <- dplyr::lag(dta$logPop, ordered_by = dta$year)
dta$lag_month <- dplyr::lag(dta$month, ordered_by = dta$year)

## Rho-transforming
rho_mile <- dta$logMilesNA - rho*dta$lagmile
rho_gas <- dta$logGasReal - rho*dta$lag_gas
rho_unem <- dta$unem - rho*dta$lag_unem
rho_pop <- dta$logPop - rho*dta$lag_pop
rho_month <- dta$month - rho*dta$lag_month

## Running rho-transformed model
rho_trans_model <- lm(rho_mile ~ rho_gas + rho_unem + rho_pop + factor(rho_month))
summary(rho_trans_model)

## 
## Call:
## lm(formula = rho_mile ~ rho_gas + rho_unem + rho_pop + factor(rho_month))
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.074031 -0.010478  0.001731  0.010546  0.065795 
## 
## Coefficients:
##                                    Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                       -1.574882   0.200142  -7.869 7.29e-14 ***
## rho_gas                           -0.054194   0.016350  -3.315 0.001035 ** 
## rho_unem                          -0.010869   0.002935  -3.704 0.000255 ***
## rho_pop                            1.660955   0.089211  18.618  < 2e-16 ***
## factor(rho_month)1.17850742580563 -0.001784   0.005161  -0.346 0.729847    
## factor(rho_month)1.35701485161126  0.185167   0.005400  34.292  < 2e-16 ***
## factor(rho_month)1.53552227741689  0.058928   0.006011   9.803  < 2e-16 ***
## factor(rho_month)1.71402970322252  0.111988   0.005249  21.336  < 2e-16 ***
## factor(rho_month)1.89253712902815  0.071313   0.004724  15.096  < 2e-16 ***
## factor(rho_month)2.07104455483379  0.096509   0.005062  19.064  < 2e-16 ***
## factor(rho_month)2.24955198063942  0.072352   0.005462  13.246  < 2e-16 ***
## factor(rho_month)2.42805940644505 -0.014690   0.005493  -2.675 0.007911 ** 
## factor(rho_month)2.60656683225068  0.098120   0.005325  18.426  < 2e-16 ***
## factor(rho_month)2.78507425805631 -0.005641   0.005067  -1.113 0.266520    
## factor(rho_month)2.96358168386194  0.061544   0.005106  12.053  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.01596 on 288 degrees of freedom
##   (1 observation deleted due to missingness)
## Multiple R-squared:  0.937,  Adjusted R-squared:  0.934 
## F-statistic: 306.1 on 14 and 288 DF,  p-value: < 2.2e-16

10.8 Estimate a dynamic model of miles driven using control variables from above. Discuss key differences.

## Distributed Lag Model
## Creating lagged miles variable
dta$lagmile <- dplyr::lag(dta$logMilesNA, ordered_by = dta$year)
reg.2.dyn <- lm(logMilesNA ~ lagmile + logGasReal + unem + logPop + factor(month) , data=dta)
summary(reg.2.dyn)

## 
## Call:
## lm(formula = logMilesNA ~ lagmile + logGasReal + unem + logPop + 
##     factor(month), data = dta)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.070624 -0.010142  0.000926  0.010416  0.063846 
## 
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)    
## (Intercept)     -1.9098039  0.3676106  -5.195 3.89e-07 ***
## lagmile          0.8064020  0.0327669  24.610  < 2e-16 ***
## logGasReal      -0.0152727  0.0052462  -2.911  0.00388 ** 
## unem            -0.0025328  0.0007938  -3.191  0.00158 ** 
## logPop           0.3376747  0.0570442   5.920 9.20e-09 ***
## factor(month)2   0.0050743  0.0049789   1.019  0.30899    
## factor(month)3   0.1910344  0.0058404  32.709  < 2e-16 ***
## factor(month)4   0.0696939  0.0046687  14.928  < 2e-16 ***
## factor(month)5   0.1185358  0.0046908  25.270  < 2e-16 ***
## factor(month)6   0.0765985  0.0053129  14.417  < 2e-16 ***
## factor(month)7   0.1062099  0.0052163  20.361  < 2e-16 ***
## factor(month)8   0.0840785  0.0056219  14.956  < 2e-16 ***
## factor(month)9  -0.0032845  0.0055601  -0.591  0.55517    
## factor(month)10  0.1083157  0.0045332  23.894  < 2e-16 ***
## factor(month)11  0.0035112  0.0047687   0.736  0.46216    
## factor(month)12  0.0696620  0.0045537  15.298  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.0159 on 287 degrees of freedom
##   (1 observation deleted due to missingness)
## Multiple R-squared:  0.9856, Adjusted R-squared:  0.9848 
## F-statistic:  1305 on 15 and 287 DF,  p-value: < 2.2e-16

## Saving the Residuals
residual_errors  <- resid(reg.2.dyn)

## Regressing Residuals
lag_err <- c(NA, residual_errors[1:(length(residual_errors)-1)])

## Residuals from Dynamic Model
plot(lag_err, residual_errors, pch=20, xlab = "Lagged Residuals", 
     ylab = "Residuals", bty="n", col="dark blue", las=1)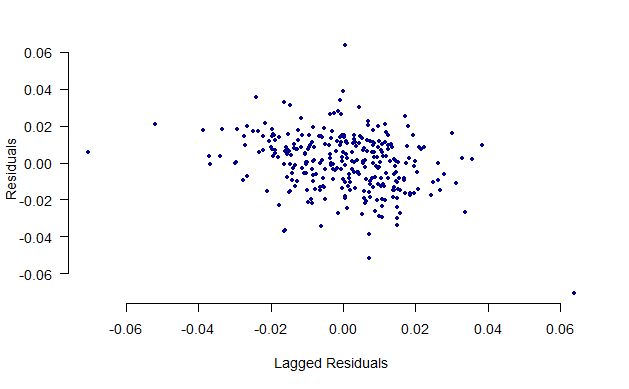

10.9 Run an Augmented Dickey-Fuller Test on logMilesNA.

## Change in miles
delta_miles <- dta$logMilesNA - dta$lagmile

## Lagged Change in Miles
lag_delta_miles <- c(NA, delta_miles[1:(length(dta$lagmile)-1)])

## Augmented Dickey-Fuller Test
aug_dickey_fuller <- lm(delta_miles ~ dta$lagmile + dta$year + lag_delta_miles)
summary(aug_dickey_fuller)

## 
## Call:
## lm(formula = delta_miles ~ dta$lagmile + dta$year + lag_delta_miles)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.14060 -0.05492  0.01217  0.03746  0.13302 
## 
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)    
## (Intercept)     -4.2949735  1.1607722  -3.700 0.000257 ***
## dta$lagmile     -0.2800211  0.0454740  -6.158 2.38e-09 ***
## dta$year         0.0038698  0.0007822   4.947 1.26e-06 ***
## lag_delta_miles -0.1450016  0.0569038  -2.548 0.011330 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.05804 on 298 degrees of freedom
##   (2 observations deleted due to missingness)
## Multiple R-squared:  0.1833, Adjusted R-squared:  0.1751 
## F-statistic:  22.3 on 3 and 298 DF,  p-value: 4.705e-13

10.10 OPTIONAL QUESTION: Conduct the same analysis from a, b, d, and g using light truck sales as the dependent variable. (Light truck sales use more gas than cars, so the question is whether gas prices affect the kind of car people buy which will affect gas consumption for the life of the car.)

## The Model
reg.lt <- lm(lttrucksales~logGasReal + unem + logPop + factor(month) , data=dta)
summary(reg.lt)

## 
## Call:
## lm(formula = lttrucksales ~ logGasReal + unem + logPop + factor(month), 
##     data = dta)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -225.99  -44.34    1.04   37.41  360.24 
## 
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)    
## (Intercept)     -21060.028   1197.027 -17.594  < 2e-16 ***
## logGasReal        -137.896     24.179  -5.703 2.91e-08 ***
## unem               -58.137      3.027 -19.208  < 2e-16 ***
## logPop            1744.238     94.889  18.382  < 2e-16 ***
## factor(month)2      59.998     21.335   2.812  0.00526 ** 
## factor(month)3     164.627     21.405   7.691 2.31e-13 ***
## factor(month)4      87.059     21.669   4.018 7.50e-05 ***
## factor(month)5     148.803     21.758   6.839 4.75e-11 ***
## factor(month)6     160.837     21.595   7.448 1.10e-12 ***
## factor(month)7     142.036     21.536   6.595 2.02e-10 ***
## factor(month)8     137.300     21.605   6.355 8.09e-10 ***
## factor(month)9      56.147     21.522   2.609  0.00956 ** 
## factor(month)10     53.670     21.480   2.499  0.01302 *  
## factor(month)11     19.991     21.357   0.936  0.35004    
## factor(month)12    108.294     21.297   5.085 6.62e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 75.41 on 289 degrees of freedom
## Multiple R-squared:  0.7722, Adjusted R-squared:  0.7612 
## F-statistic: 69.98 on 14 and 289 DF,  p-value: < 2.2e-16

## Saving the Residuals
dta$residual_errors  <- resid(reg.lt)

## Regressing Residuals
lag_err <- c(NA, dta$residual_errors[1:(length(dta$residual_errors)-1)])

plot(lag_err, dta$residual_errors, pch=20, xlab = "Lagged Residuals", 
     ylab = "Residuals", bty="n", col="dark blue", las=1)
abline(lm(dta$residual_errors ~ lag_err), lwd=2)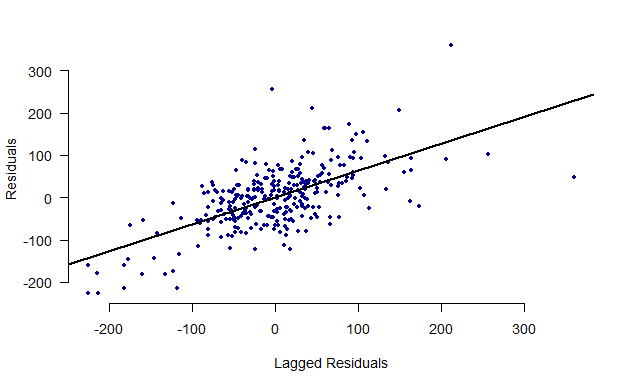

## Plotting Over Time
plot(dta$residual_errors, pch=20, xlab = "Time", las=1, 
     ylab = "Residuals", bty="n", col="dark blue")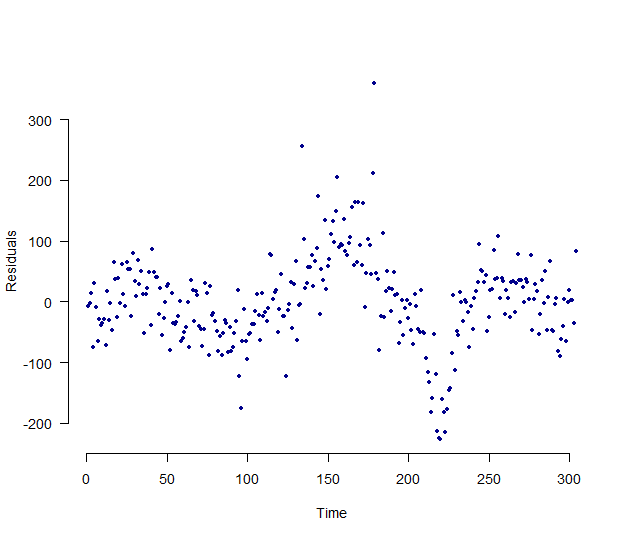

# Creating season category and plotting residual error
dta %>% 
  ggplot() +
  geom_line(aes(x=as.Date(date), y=residual_errors, col=season), size=.8) +
  scale_color_manual(values=c("orange", "green", "red", "darkblue"))+
  labs(x="Date", y="Residual Errors") +
  theme_classic() +
  theme(panel.grid.major.y=element_line(color="darkgrey", linetype="dotted"), panel.grid.minor.y=element_line(color="darkgrey", linetype="dotted")) %>%
  labs(col="Season")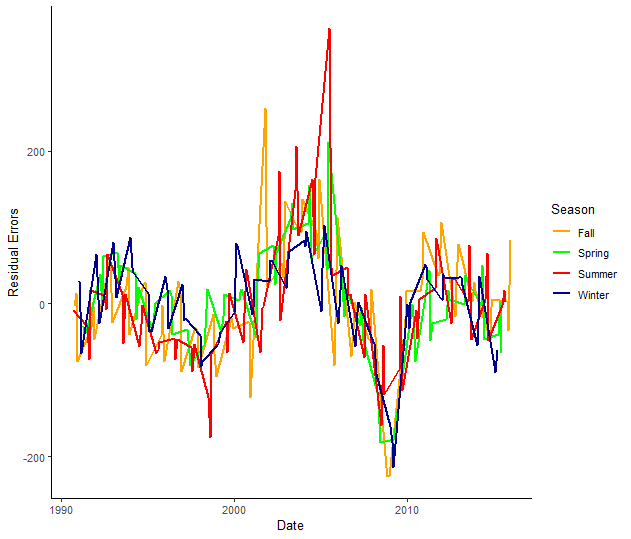

# Creating season category and plotting residual error
dta %>% 
  ggplot() +
  geom_point(aes(x=as.Date(date), y=residual_errors, col=season)) +
  scale_color_manual(values=c("orange", "green", "red", "darkblue"))+
  labs(x="Date", y="Residual Errors") +
  theme_classic() +
  theme(panel.grid.major.y=element_line(color="darkgrey", linetype="dotted"), panel.grid.minor.y=element_line(color="darkgrey", linetype="dotted")) %>%
  labs(col="Season")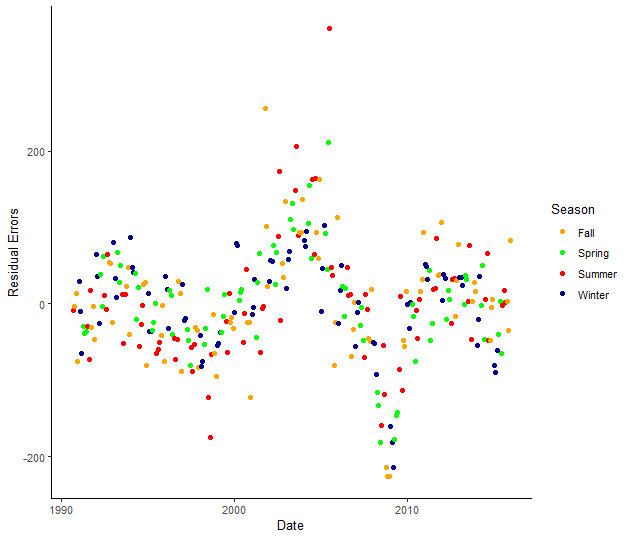

## Cochrane-Orcutt Model
reg.orc2 <- cochrane.orcutt(reg.lt)
summary(reg.orc2)

## Call:
## lm(formula = lttrucksales ~ logGasReal + unem + logPop + factor(month), 
##     data = dta)
## 
##                    Estimate  Std. Error t value  Pr(>|t|)    
## (Intercept)     -21271.4536   2398.4045  -8.869 < 2.2e-16 ***
## logGasReal        -148.4413     44.3120  -3.350 0.0009162 ***
## unem               -52.5199      6.2014  -8.469 1.286e-15 ***
## logPop            1758.1619    190.3266   9.238 < 2.2e-16 ***
## factor(month)2      60.0153     12.8791   4.660 4.842e-06 ***
## factor(month)3     165.6953     16.7822   9.873 < 2.2e-16 ***
## factor(month)4      91.0501     19.7436   4.612 6.016e-06 ***
## factor(month)5     152.7067     21.0327   7.260 3.611e-12 ***
## factor(month)6     162.2202     20.8922   7.765 1.442e-13 ***
## factor(month)7     143.1172     20.8265   6.872 3.920e-11 ***
## factor(month)8     139.6807     20.9328   6.673 1.285e-10 ***
## factor(month)9      60.0386     20.7456   2.894 0.0040938 ** 
## factor(month)10     57.8695     19.6575   2.944 0.0035051 ** 
## factor(month)11     23.3824     17.4432   1.340 0.1811433    
## factor(month)12    111.1238     13.9218   7.982 3.451e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 57.3085 on 298 degrees of freedom
## Multiple R-squared:  0.6307 ,  Adjusted R-squared:  0.6258
## F-statistic: 35.1 on 4 and 298 DF,  p-value: < 4.603e-54
## 
## Durbin-Watson statistic 
## (original):    0.72932 , p-value: 1.646e-28
## (transformed): 2.33482 , p-value: 9.971e-01