8 Lab VII: Interactions & Categorical Variables

8.1 Categorical Variables and Reference Categories

8.1.1 Loading Data

load("~/GOVT5001/Lab VII/social.RData")

8.1.2 The Four Categories of the Treatment Variable

unique(social$messages)
## [1] "Civic Duty" "Hawthorne"  "Control"    "Neighbors"

8.1.3 Estimating the Model

reg1 <- lm(primary2006~messages, data=social)

8.1.4 Difference in Means Between Categories

reg1$coefficients[1]
## (Intercept) 
##   0.3145377
reg1$coefficients[2]
## messagesControl 
##     -0.01789934
reg1$coefficients[3]
## messagesHawthorne 
##       0.007836968
reg1$coefficients[4]
## messagesNeighbors 
##        0.06341057

8.1.5 Changing the Reference Category

social$messages <- as.factor(social$messages)

reg2 <- lm(primary2006~relevel(messages, "Control"), 
           data=social)

reg2$coefficients[1]
## (Intercept) 
##   0.2966383
reg2$coefficients[2]
## relevel(messages, "Control")Civic Duty 
##                             0.01789934
reg2$coefficients[3]
## relevel(messages, "Control")Hawthorne 
##                            0.02573631
reg2$coefficients[4]
## relevel(messages, "Control")Neighbors 
##                            0.08130991

8.2 Interactions

  • How to use interactions
    • In R
      • lm(y~x*z, data=data) or lm(y~x + z + x:z, data=data)
  • We write a model with an interaction term as:

\[\hat{Y_i}=\hat{\beta_0} + \hat{\beta_1}X_i + \hat{\beta_2}Z_i + \hat{\beta_3}(X_i*Z_i)\]

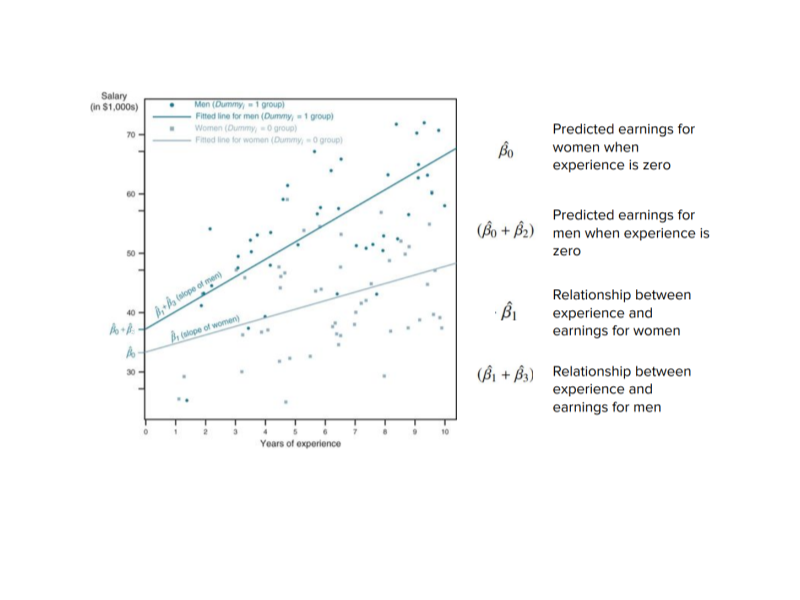
8.2.1 Interpreting Interactions

\[\hat{Wage_i}=\hat{\beta_0} + \hat{\beta_1}Experience_i + \hat{\beta_2}Male_i + \hat{\beta_3}Experience_i*Male_i\]

  • \(\beta_0\) - Predicted wage for women with no experience

  • \(\beta_0 + \beta_1\) - Relationship between experience and earnings for women

  • \(\beta_0 + \beta_1 + \beta_2 + \beta_3\) - Predicted Wage for men with experience

  • \(\beta_1\) - The effect of experience for women

  • \(\beta_0 + \beta_2\) - Predicted earnings for men when experience is zero

  • \(\beta_1 + \beta_3\) - Relationship between experience and earnings for men

8.3 Lab Questions

8.3.1 What is the effect of age on support for Trump, conditional on being a Republican? Do this with both the colon, “:”, and the “*“.

model1a <- lm(TrumpFT~Rep*Age, data=dta)
model1a
## 
## Call:
## lm(formula = TrumpFT ~ Rep * Age, data = dta)
## 
## Coefficients:
## (Intercept)      RepTRUE          Age  RepTRUE:Age  
##     13.1949      21.1904       0.0509       0.3780
model1b <- lm(TrumpFT~Rep + Age + Rep:Age, data=dta)
model1b
## 
## Call:
## lm(formula = TrumpFT ~ Rep + Age + Rep:Age, data = dta)
## 
## Coefficients:
## (Intercept)      RepTRUE          Age  RepTRUE:Age  
##     13.1949      21.1904       0.0509       0.3780

8.3.2 What is the effect of age on support for Trump, conditional on being a Democrat?

model2a <- lm(TrumpFT~Dem*Age, data=dta)
model2a
## 
## Call:
## lm(formula = TrumpFT ~ Dem * Age, data = dta)
## 
## Coefficients:
## (Intercept)      DemTRUE          Age  DemTRUE:Age  
##     22.5503      -9.3525       0.5281      -0.5749
model2b <- lm(TrumpFT~Dem + Age + Dem:Age, data=dta)
model2b
## 
## Call:
## lm(formula = TrumpFT ~ Dem + Age + Dem:Age, data = dta)
## 
## Coefficients:
## (Intercept)      DemTRUE          Age  DemTRUE:Age  
##     22.5503      -9.3525       0.5281      -0.5749

8.3.3 Interpret the following plot.

plot(dta$Age, dta$TrumpFT, color=dta$Rep, col=c("red", "blue"), 
     main="The Effect of Age on Support for Trump Conditional on Party ID",
     xlab = "Age", ylab = "Trump FT", las=1, xlim=c(0,100), pch="")
abline(lm(TrumpFT~Age, data = subset(dta, Rep==TRUE)), col="dark red", lwd=3)
abline(lm(TrumpFT~Age, data = subset(dta, Dem==TRUE)), col="dark blue", lwd=3)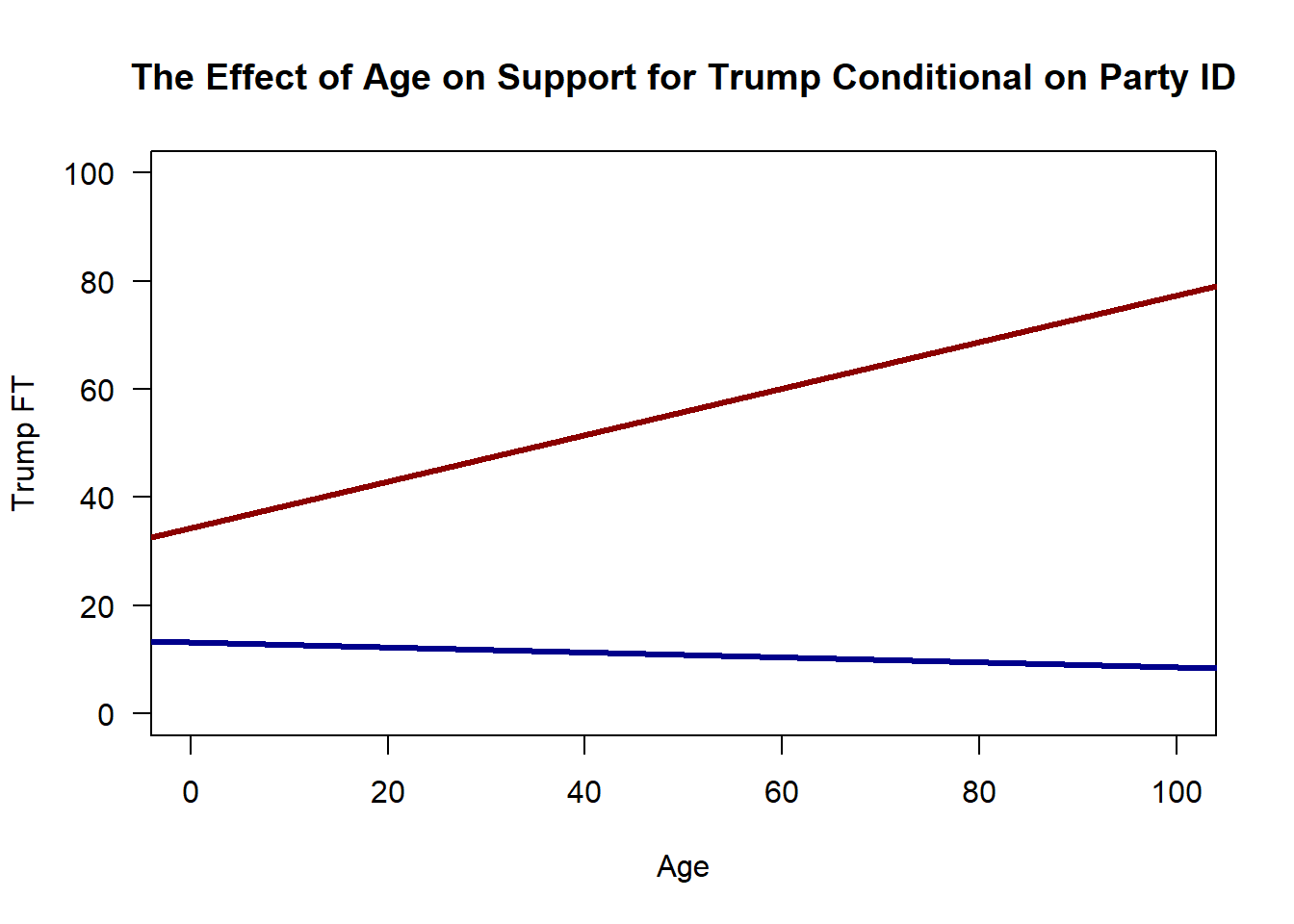

8.3.4 What are your predictions for how women may feel about Clinton, how Democrats may feel about Clinton, and how Democratic women may feel about Clinton? Then estimate the model.

Most answers will be good here. The idea is just to think about conditional effects. For example, women may approve more of Clinton because she could have been the first woman president. Democrats probably approve of Clinton because she was the Democratic nominee for president. Democratic women, then, may support Clinton EVEN more than Republican women and Democratic men. The conditional effect of being a Democrat for women will be positive.

model3 <- lm(ClintonFT~Female*Dem, data=dta)
model3
## 
## Call:
## lm(formula = ClintonFT ~ Female * Dem, data = dta)
## 
## Coefficients:
##    (Intercept)          Female         DemTRUE  Female:DemTRUE  
##         17.690           1.114          27.621           6.882

8.3.5 How do we interpret the following:

  • Intercept = Clinton Feelings for Male Republicans

  • Intercept + Beta 1 = Clinton Feelings for Female Republicans

  • Intercept + Beta 2 = Clinton Feelings for Male Democrats

  • Intercept + Beta 1 + Beta 2 + Beta 3 = Clinton Feelings for Female Democrats

  • Beta 1 - The Effect of Sex for Republicans

  • Beta 2 - The Effect of Party for Men

  • Beta 2 + Beta 3 - The Effect of Party for Women

  • Beta 1 + Beta 3 - The Effect of Sex for Democrats

8.3.6 Estimate the the same model as above, but for Trump and Republicans.

model4 <- lm(TrumpFT~Female*Rep, data=dta)
model4
## 
## Call:
## lm(formula = TrumpFT ~ Female * Rep, data = dta)
## 
## Coefficients:
##    (Intercept)          Female         RepTRUE  Female:RepTRUE  
##         19.134          -8.887          33.196           5.965

8.3.7 Calculate the following:

  • What is Trump’s average feeling for male Democrats? - 19.134

  • What is Trump’s average feeling for female Democrats? - 10.247

  • What is Trump’s average feeling for male Republicans? - 52.33

  • What is Trump’s average feeling for female Republicans? - 49.408