10 Lab IX Interactions Redux
## Data
load("~/GOVT8001/Lab 10/Ch12_Exercise2_Global_warming.RData")
## Packages
library(tidyverse)
library(margins)10.1 Review of Interactions
- Baseline Model
- Consider the following model that regresses beliefs in human caused global warming on education, race, and political ideology
\[Human\ Cause_i = \alpha + \beta_1 Educ_i + \beta_2 White_i + \beta_3 Party7_i + \epsilon_i\]
party7is a 7 point ideological scale ranging from 0, most conservative, to 7, most liberal.- Interpret the following coefficients
##
## Call:
## lm(formula = humancause ~ educ + white + party7, data = dta)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.6677 -0.3461 -0.1502 0.4478 1.0551
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.410810 0.070554 -5.823 0.00000000681 ***
## educ 0.029916 0.005207 5.745 0.00000001072 ***
## white 0.030842 0.024806 1.243 0.214
## party7 0.085558 0.005060 16.909 < 0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4359 on 1851 degrees of freedom
## (17 observations deleted due to missingness)
## Multiple R-squared: 0.1501, Adjusted R-squared: 0.1488
## F-statistic: 109 on 3 and 1851 DF, p-value: < 0.00000000000000022- Now let’s interact
whitewithparty7\[Human\ Cause_i = \alpha + \beta_1 Educ_i + \beta_2 White_i + \beta_3 Party7_i + \beta_4 (White_i \times Party7_i) + \epsilon_i\] - Interpret the following coefficients
##
## Call:
## lm(formula = humancause ~ educ + white * party7, data = dta)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.7074 -0.3523 -0.1280 0.4208 1.0921
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.17303 0.08618 -2.008 0.044829 *
## educ 0.03066 0.00518 5.920 0.00000000383 ***
## white -0.26183 0.06638 -3.944 0.00008298417 ***
## party7 0.03761 0.01128 3.334 0.000874 ***
## white:party7 0.05987 0.01261 4.749 0.00000220205 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4333 on 1850 degrees of freedom
## (17 observations deleted due to missingness)
## Multiple R-squared: 0.1604, Adjusted R-squared: 0.1586
## F-statistic: 88.34 on 4 and 1850 DF, p-value: < 0.0000000000000002210.2 library(margins)
model1 <- lm(humancause ~ educ + white + party7, data = dta)
margins(model1)## educ white party7
## 0.02992 0.03084 0.08556model1##
## Call:
## lm(formula = humancause ~ educ + white + party7, data = dta)
##
## Coefficients:
## (Intercept) educ white party7
## -0.41081 0.02992 0.03084 0.08556summary(margins(model1))## factor AME SE z p lower upper
## educ 0.0299 0.0052 5.7451 0.0000 0.0197 0.0401
## party7 0.0856 0.0051 16.9088 0.0000 0.0756 0.0955
## white 0.0308 0.0248 1.2433 0.2137 -0.0178 0.0795- You can select specific variables
summary(margins(model1, variables = "white"))## factor AME SE z p lower upper
## white 0.0308 0.0248 1.2433 0.2137 -0.0178 0.0795- Now with the interaction term included
- See the different marginal effects
- This is useful if you want to see the marginal effect at representative cases (MER) or the marginal effect at the mean (MEM)
model2 <- lm(humancause ~ educ + white*party7, data = dta)
summary(margins(model2, at = list(white = 0:1)))## factor white AME SE z p lower upper
## educ 0.0000 0.0307 0.0052 5.9198 0.0000 0.0205 0.0408
## educ 1.0000 0.0307 0.0052 5.9198 0.0000 0.0205 0.0408
## party7 0.0000 0.0376 0.0113 3.3337 0.0009 0.0155 0.0597
## party7 1.0000 0.0975 0.0056 17.3388 0.0000 0.0865 0.1085
## white 0.0000 -0.0139 0.0264 -0.5260 0.5989 -0.0656 0.0379
## white 1.0000 -0.0139 0.0264 -0.5260 0.5989 -0.0656 0.0379summary(margins(model2, variables = "white", at = list(party7 = 0:7)))## factor party7 AME SE z p lower upper
## white 0.0000 -0.2618 0.0664 -3.9444 0.0001 -0.3919 -0.1317
## white 1.0000 -0.2020 0.0549 -3.6803 0.0002 -0.3095 -0.0944
## white 2.0000 -0.1421 0.0440 -3.2309 0.0012 -0.2283 -0.0559
## white 3.0000 -0.0822 0.0343 -2.3989 0.0164 -0.1494 -0.0150
## white 4.0000 -0.0224 0.0271 -0.8259 0.4089 -0.0755 0.0307
## white 5.0000 0.0375 0.0247 1.5177 0.1291 -0.0109 0.0859
## white 6.0000 0.0974 0.0284 3.4326 0.0006 0.0418 0.1529
## white 7.0000 0.1572 0.0363 4.3332 0.0000 0.0861 0.2283- Let’s consider a continuous interaction
model3 <- lm(humancause ~ educ*party7, data = dta)
summary(model3)##
## Call:
## lm(formula = humancause ~ educ * party7, data = dta)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.8379 -0.2923 -0.1515 0.4413 0.9783
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.45181 0.15279 2.957 0.003146 **
## educ -0.03694 0.01215 -3.041 0.002388 **
## party7 -0.10965 0.03192 -3.435 0.000605 ***
## educ:party7 0.01558 0.00254 6.134 0.00000000105 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4317 on 1851 degrees of freedom
## (17 observations deleted due to missingness)
## Multiple R-squared: 0.1664, Adjusted R-squared: 0.165
## F-statistic: 123.1 on 3 and 1851 DF, p-value: < 0.00000000000000022summary(margins(model3, variables = "party7", at = list(educ = 0:16)))## factor educ AME SE z p lower upper
## party7 0.0000 -0.1096 0.0319 -3.4354 0.0006 -0.1722 -0.0471
## party7 1.0000 -0.0941 0.0294 -3.1986 0.0014 -0.1517 -0.0364
## party7 2.0000 -0.0785 0.0269 -2.9171 0.0035 -0.1312 -0.0258
## party7 3.0000 -0.0629 0.0244 -2.5770 0.0100 -0.1108 -0.0151
## party7 4.0000 -0.0473 0.0219 -2.1585 0.0309 -0.0903 -0.0044
## party7 5.0000 -0.0318 0.0195 -1.6319 0.1027 -0.0699 0.0064
## party7 6.0000 -0.0162 0.0170 -0.9510 0.3416 -0.0495 0.0172
## party7 7.0000 -0.0006 0.0146 -0.0411 0.9672 -0.0292 0.0280
## party7 8.0000 0.0150 0.0122 1.2253 0.2205 -0.0090 0.0389
## party7 9.0000 0.0306 0.0099 3.0735 0.0021 0.0111 0.0500
## party7 10.0000 0.0461 0.0078 5.8998 0.0000 0.0308 0.0615
## party7 11.0000 0.0617 0.0060 10.2359 0.0000 0.0499 0.0735
## party7 12.0000 0.0773 0.0049 15.6305 0.0000 0.0676 0.0870
## party7 13.0000 0.0929 0.0050 18.4070 0.0000 0.0830 0.1028
## party7 14.0000 0.1084 0.0063 17.2860 0.0000 0.0962 0.1207
## party7 15.0000 0.1240 0.0081 15.2475 0.0000 0.1081 0.1400
## party7 16.0000 0.1396 0.0103 13.5678 0.0000 0.1194 0.159810.3 Marginal Effects Plots
- Let’s consider a continuous interaction plot
c <- cplot(model3, "educ", "party7", what = "effect")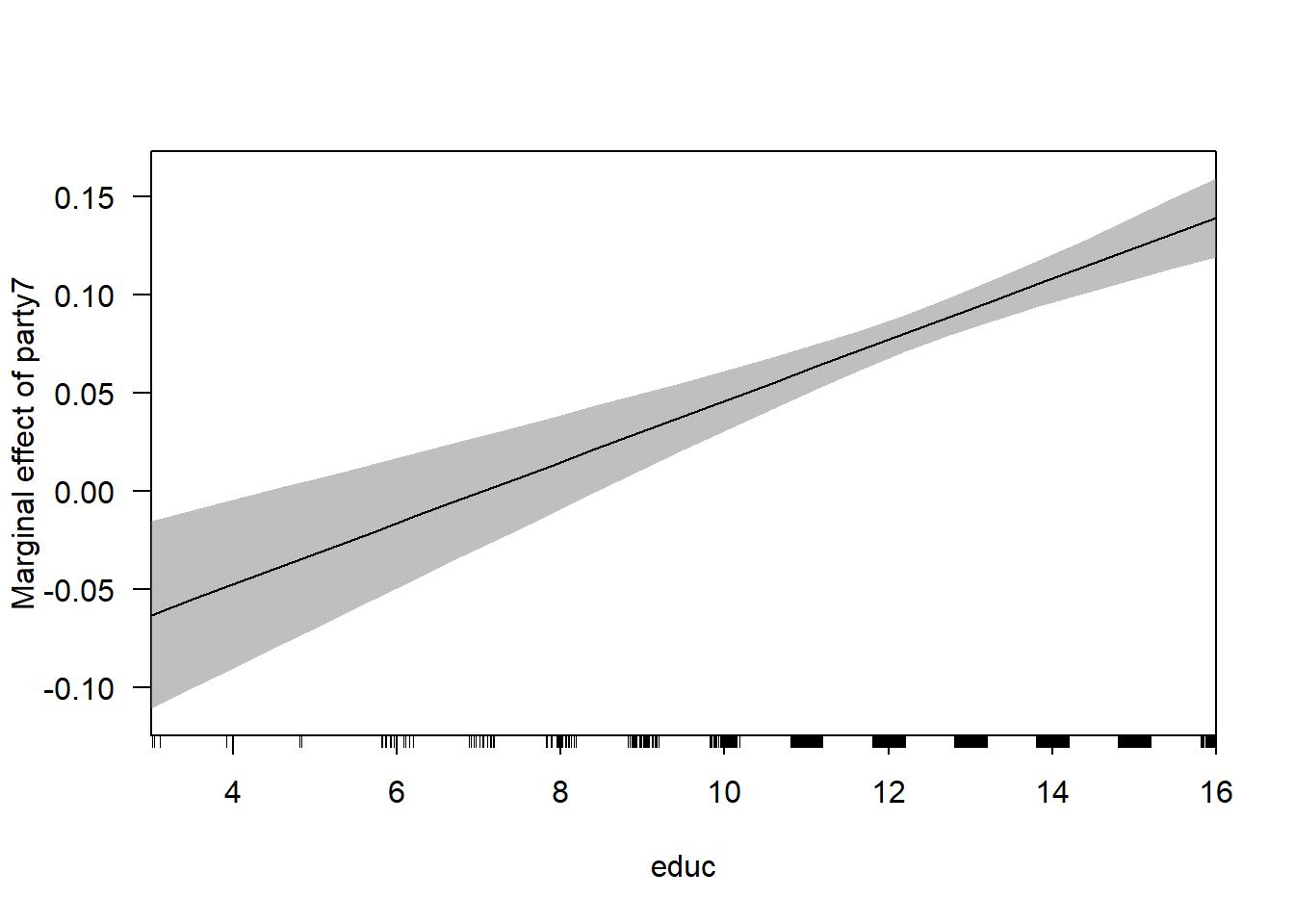
ggplot(c, aes(x = xvals)) +
geom_line(aes(y = yvals)) +
geom_line(aes(y = upper), linetype = 2) +
geom_line(aes(y = lower), linetype = 2) +
geom_hline(yintercept = 0) +
ggtitle("Effect of Becoming More Liberal By Education") +
xlab("Education") + ylab("AME party7") + theme_bw()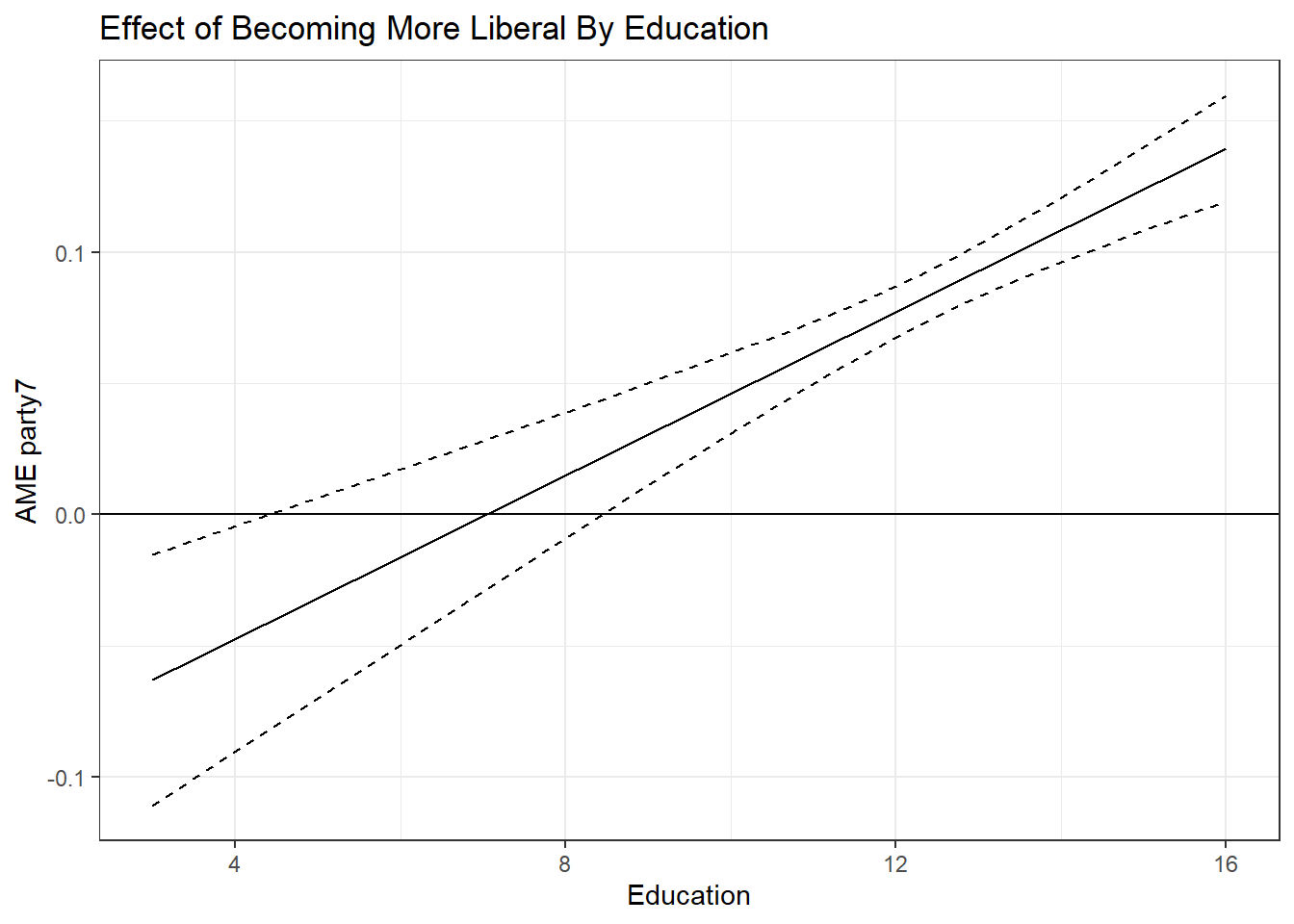
- Let’s consider a model with a squared term \[Human\ Cause_i = \alpha + \beta_1 Age_i + \beta_2 Age_i^2 + \epsilon_i\]
model4 <- lm(humancause ~ age + I(age^2), data = dta)
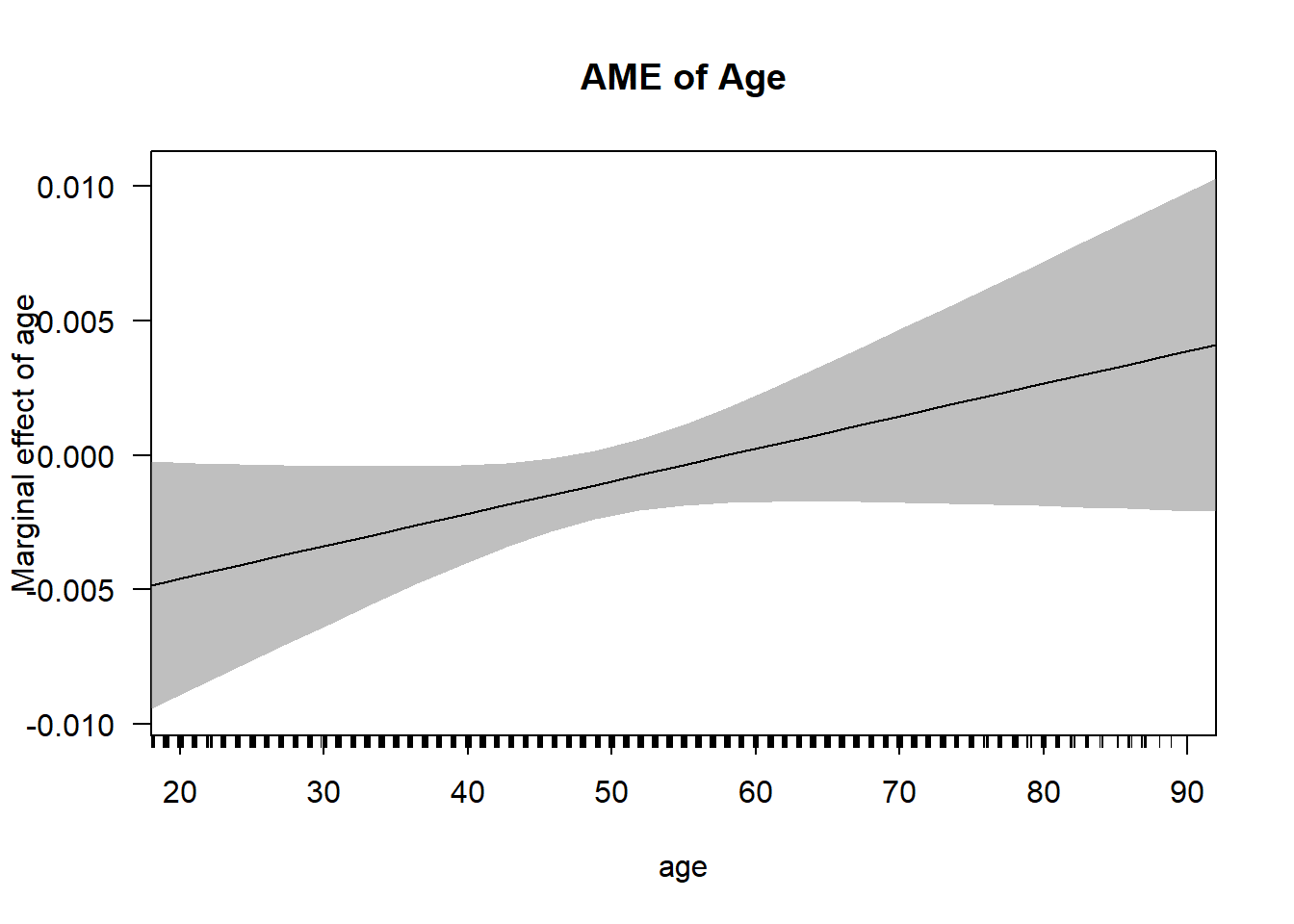
summary(margins(model4, variables = "age", at = list(age = c(20, 40, 60, 80))))## factor age AME SE z p lower upper
## age 20.0000 -0.0046 0.0022 -2.0836 0.0372 -0.0089 -0.0003
## age 40.0000 -0.0022 0.0009 -2.3593 0.0183 -0.0040 -0.0004
## age 60.0000 0.0002 0.0010 0.2386 0.8114 -0.0017 0.0022
## age 80.0000 0.0027 0.0023 1.1461 0.2518 -0.0019 0.0072cplot(model4, "age", what = "effect", main = "AME of Age")